All text and images on this post are from the links provided and can be found here. All text is by Peter Pesic in relation to his work Music and the making of modern science.
By Peter Pesic
Many people interested in science are also keenly interested in music, and vice versa. But what is the connection between music and science? To a surprising degree, science has been influenced significantly by music. Let me present three important historical examples, ending with a notable recent discovery.
This influence goes back to the very beginnings of science in ancient Greece. There, the followers of Pythagoras found that music gave the first link between natural phenomena and mathematics, two realms previous considered unrelated (figure 1). The Pythagoreans noticed that familiar musical intervals were produced by strings whose lengths formed simple whole-number ratios, such as the octave (2:1) and the perfect fifth (3:2). For them, this was the first revelation of how “all is number,” providing the first step in their ambitious program to understand everything using mathematics. Plato took up this program and presented an account of the cosmos as being formed according to musical ratios. In contrast, his student Aristotle argued that number was too rigid and unchanging to describe the organic processes of growth and change that were crucial to what he called “physics.” Indeed, Aristotle’s Physics founded that field and was its main text for over a millennium.

Figure 1. Images of the founders of music from Francinus Gaffurius, Theorica musicae (1492): Jubal, from the Bible (top left), along with images of Pythagoras (trying bells, glasses, and pipes) and Philolaus.
Drawing on Pythagorean ideas, Plato advanced a whole new conception of education going beyond rote memorization to the study of seven “liberal arts” (as they came to be called), comprising three basic linguistic arts (grammar, logic, rhetoric) and four mathematical arts (arithmetic, geometry, music, astronomy). These mathematical sister arts became known as the quadrivium, the “four-fold way” that became the heart of higher education (figure 2). As I argue in my book Music and the Making of Modern Science, our natural sciences are the “children” of this divine sisterhood, in which music was an essential part, bridging the purely mathematical (arithmetic and geometry) and the visible (such as astronomy).
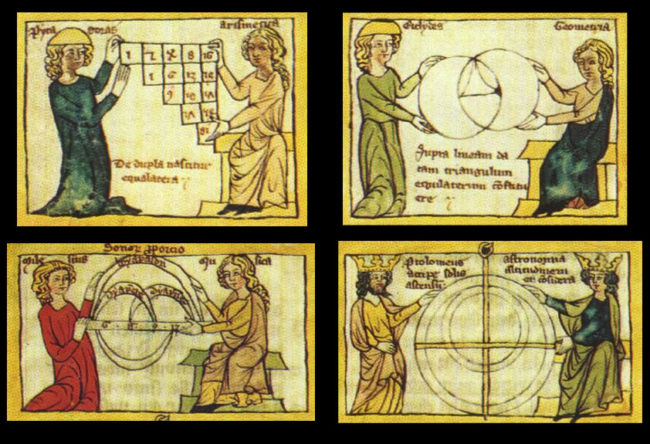
Figure 2. The quadrivium, the “four-fold path” encompassing the four sister studies central to higher “liberal education”: arithmetic, geometry, music, and astronomy.
Higher education to this day still reflects Plato’s radical plan, even though most people do not know what the “liberal arts” really were or meant. As late as the time of Isaac Newton, university students studied the classic texts that had over centuries come to represent those arts. For instance, the young Johannes Kepler studied Boethius’s Institutes of Music alongside Aristotle’s Physics. From an early age, Kepler sang and heard music as well as studied its theory. Though he disclaimed any expertise in composition or performance, music was extraordinarily important to him. His Harmony of the World (1619) sought to modernize Plato’s musical vision of the cosmos using the latest astronomical observations made by Tycho Brahe. In that book, Kepler used Tycho’s data to reconstruct the real songs of the planets and the kind of many-voiced musical polyphony (of which he thought the ancient Greeks ignorant) of their various individual songs (figure 3).
Figure 3. The planetary songs (including the moon) as calculated by Johannes Kepler in his Harmonices mundi (1619), using the data of Tycho Brahe.
As an ardent Copernican, Kepler emphasized that now the Earth, no longer stationary, had a song like all the other planets. He calculated that the Earth’s song was a melancholy semitone, MI FA MI, endlessly repeated, which he interpreted as singing “Miseria et Fames,” misery and famine. Living in a time of continual religious war and suffering himself persecution from both Catholics and Protestants, Kepler thought the Earth’s song was all too apt, all too accurately expressing (if not actually influencing) terrestrial misery.
Kepler’s interest in music included familiarity with great composers of his time, especially Orlando di Lasso. Trying to understand the dissonant harmonies of the planets, Kepler invites the composers of his time to write a motet that would show how those dissonances could be resolved. Several times he mentions Lasso’s motet ““In me transierunt,” whose opening notes (in then-current notation) was spelled MI FA MI (figure 4). Thus, this composition could well have struck Kepler as a beautiful representation of the mournful song of the Earth.
Figure. 4. The opening measures of Orlando di Lasso’s motet In me transierunt as transcribed by Kepler and in a modern score.
Kepler’s musical investigations led to an important astronomical discovery that became known as his third (or “harmonic”) law of planetary motion: the squares of the periods of any planet is proportional to the cube of its mean distance from the sun. Kepler announced this result with great excitement: since his youth he had been seeking such a deep relation connecting the orbits of different planets, but only Tycho’s precise observations allowed him to discover it. Kepler’s connection of squares and cubes (second and third powers) reminds us of the Pythagorean ratio for a fifth (3:2); he only discovered it in the course of looking for such musical ratios in different planetary data.
Kepler’s harmonic law was of the greatest importance for Isaac Newton, who used it in his Principia (1687) to give a decisive argument for the inverse square law of gravitation. As an undergraduate, Newton himself had studied Boethius, the classic liberal arts musical text, on which he commented in detailed notes (figure 5). In later life, he liked to remark that “Pythagoras’s Musick of the Spheres was gravity.”

Figure. 5. A page from Isaac Newton’s undergraduate notebook, dated November 1665, showing “ye distances of any two notes.” (Courtesy of The Syndics of The Cambridge University Library).
In experiments he began in early youth, Newton showed that white light was composed of a full spectrum of colors. He decided that spectrum spanned an octave in color, imposing the analogy of music onto light because he thought violet was a “recurrence” of deep red (he called it “purple”) in the same way that one D sounds akin to the D an octave higher. He took this analogy so seriously that he decided to name the colors in the spectrum in accord with the seven notes between one D and another (figure 6). To make this work, Newton had to introduce into the spectral colors orange and indigo to fill out a seven-note “keyboard” comprising Red Orange Yellow Green Blue Indigo Violet—the mnemonic ROY G BIV that everyone now learns as “the” colors in the spectrum. Many people find it difficult to differentiate orange from yellow or indigo from blue, and that’s no accident: Newton inserted them to enforce his musical analogy while admitting that the colors in the spectrum are somewhat arbitrary. But such remains the force of his authority that many people do not realize the curious musical backstory behind these colors.
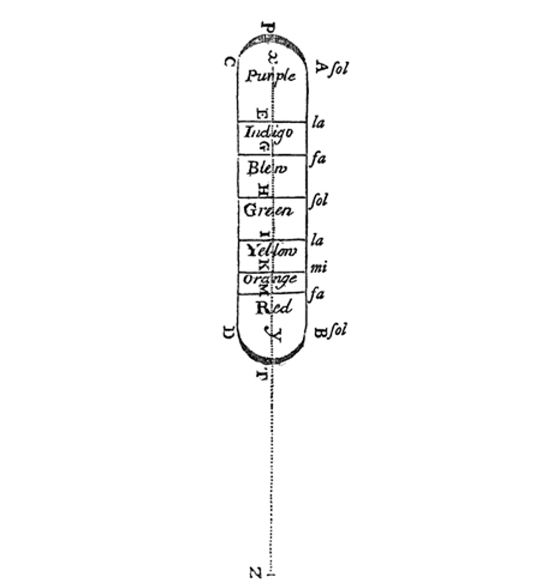
Figure 6. Newton’s illustration (1675) of the analogy between spectral colors and the seven notes of the diatonic scale. The note names follow the older nomenclature spelling the Dorian mode.
The note names follow the older nomenclature spelling the Dorian mode.That story has a curious epilogue. In his later work on the colors seen when lenses are pressed together—“Newton’s rings”—Newton realized that the color spectrum did not really span an octave (2:1) but more nearly 9:14, about major sixth, like the interval between D and the B above it (figure 7). He tried to explain this discrepancy away, curiously enough by using an argument that involved square and cubes in a way reminiscent of Kepler’s harmonic law of planetary motion. But though Newton obviously recognized a problem, he never went back to revise his views on the octave he had imposed on the spectrum since his earliest work. If he had, he might have found crucial evidence that would demonstrate the wave theory of light rather than the particle theory that Newton generally maintained. Had he cared to look, that ratio of a major sixth could have told him the ratio of the wavelengths of red to violet light (400:700 nanometers, in modern units). Though Newton took music seriously, perhaps he did not take it seriously enough. If he had, he might have advanced the wave theory of light a century; as it was, only about 1800 did Thomas Young give definitive evidence for that theory, during which he commented upon Newton’s mistake (which Leonhard Euler had also noticed earlier).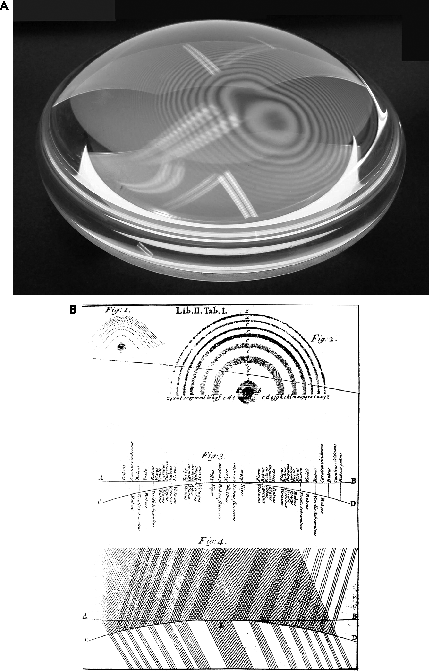
Figure 7. Newton’s rings. (a) a modern recreation of his experiment using two plano-convex lenses pressed against each other, showing the characteristic moiré pattern; (b) Newton’s diagrams of the rings from his Opticks (1704).
For my final historical example, let me leap forward another century to Max Planck, who first introduced the quantum in 1900 and thereby began the most consequential shift in modern physics. Like many other German scientists, Planck was a Kulturträger—a “bearer of culture,” someone steeped in literature and especially music. Planck played the piano, conducted, composed, even thought of becoming a professional musician. He studied physics particularly for its philosophical qualities and what he considered its “search for the absolute,” for universal laws of nature. As a young man, he spent a year in Berlin with Hermann von Helmholtz, himself an exemplary Kulturträger who was both physician and physicist, a passionate musician who had written the great works on physiological optics and on acoustics (figure 8). Indeed, during Planck’s year with him (1877) Helmholtz published the fourth and final edition of his masterwork On the Sensations of Tone as a Physiological Basis for the Theory of Music. Planck surely spent many evenings at his mentor’s home enjoying their mutual passion for music.
Figure 8. Hermann von Helmholtz, painted by Ludwig Knaus in 1881. The table shows both his opthalmoscope as well as acoustic instruments, such as the round resonator.
When Planck was called to Berlin as professor of physics (1893), he was tasked with studying a new Eitz harmonium that Helmholtz had ordered, an innovative instrument capable of dividing an octave into 104 parts (figure 9), compared to the twelve of a standard keyboard. This assignment in itself shows how important music was to the work of the Berlin physics department in Planck’s time. Planck was fascinated by this harmonium; even its daunting keyboard he learned to play “with a little practice,” as he modestly put it. Using it, he could test out Helmholtz’s theories that “natural tuning”—based on simple whole-number ratios that were the heir to the Pythagorean intervals—was superior to “equal temperament,” then as now the standard by which pianos and organs were tuning using irrational numbers to equalize all twelve steps in the scale.
Indeed, Helmholtz was passionate in his advocacy of natural temperament (now generally called “just intonation”). He invited great musicians such as Johannes Brahms and Joseph Joachim to his house to play his harmoniums for them and elicit their agreement that equal temperament had ruined music. Brahms, notoriously gruff, refused to agree and privately called Helmholtz “an enormous dilettante.” Helmholtz persevered despite such opposition; though he did not make much headway in his own time, now performances of older music try to use the historically correct temperaments, not just the equal temperament that only became widespread during the nineteenth century. Then too, unaccompanied vocal ensembles like barbershop quartets will approach “natural tuning” as they strive for particularly close harmony.
Planck was fascinated by these ideas and decided to make an experimental test of Helmholtz’s pet idea. In fact, this was the only experiment Planck ever performed; he was a theoretical physicist, one of the first to hold a position specifically in that field, as opposed to the mixture of experiment and theory that had previously been the norm. Planck decided to write short compositions to test whether “natural tuning” really was more natural than equal temperament. He constructed a four-part piece for unaccompanied voices so that if the singers really were tracking the “natural” intervals (not using a piano to enforce equal temperament), by the end of the piece the choir would have sunk down an entire half-step in pitch (figure 10).
Figure 10. Max Planck’s first composition to test Helmholtz’s theory about singers’ preferences for “natural” versus equal tuning.
Fully expecting Helmholtz’s theory to be borne out in practice, Planck was quite surprised when the singers kept their original pitch steady, instead of dropping it as the “natural tuning” would have dictated. Following good experimental procedure, he also constructed another test piece in which the pitch should have risen a half-step if the singers were following “natural tuning”: again they stayed true to the piano, even though singing unaccompanied. Planck concluded that habit was stronger than “nature”: growing up hearing pianos play in equal temperament (and having choral directors insist on holding those pitches steady), the singers were influenced more by those long-established habits than by the presumably “natural” desire to sing in close harmony. Planck published these results in a musicological journal, though they long remained unknown because they were not included among his other scientific papers.
One can only wonder what Helmholtz would have made of this startling contradiction to his cherished theory, but he had far worse problems: after a sudden fall, he died in 1894, “the black year of German physics” in which Planck’s colleagues Heinrich Hertz and August Kundt also died. As the sole surviving professor of physics in Berlin, Planck had to set aside his work on the harmonium and take up other projects. The German lighting industry was pressing for practical help to design optimal light bulbs, which involved investigating the laws of radiation by heated bodies that were studied experimentally in Berlin. Planck’s interest in finding absolute laws of nature, especially in relation to thermodynamics, led him to address these new experimental findings. His autobiography passes directly from his work on the harmonium to his work on black-body radiation and the quantum postulate Planck put forward to explain his colleagues’ experiments.
Thinking back to the analogy between color and sound, one might say that Planck was trying to find the “natural tuning” that governed the spaces between the allowed colors of a heated body considered as if those shades were adjacent “keys” of a cosmic harmonium. Planck broke the spectrum of light from a heated body into equal steps according to his now-famous formula E = hν, where E is the energy of the light, ν its frequency, and h a new constant of nature that essentially specified the size of the interval between the “keys.” As he told his son Erwin at the time, Planck felt that his discovery was momentous because he had found “natural units” of length and time that would hold throughout the universe and could be recognized by any species of intelligent beings. These natural units showed that light obeyed an absolute and “natural tuning” that was at the same time perfectly equal because of the equal energy steps between the keys: hν, 2hν, 3hν, 4hν,… Though Planck did not explicitly draw attention to this correspondence, it is hard to imagine that this perceptive man did not notice that his work managed to reconcile the natural with the equal in the realm of light, even though in the music he studied “natural tuning” was at odds with “equal temperament.” By telling the story of the harmonium next to that of black-body radiation, Planck’s autobiography certainly invites us to consider their relation.
The interaction between music and science continues to evolve in ways that show their close relation over many centuries. Today, particle physicists find what they call “resonances,” a term that directly reminds us of the resonant vibrations of bodies, going back all the way to the vibrating glasses already used by the Pythagoreans so long ago (figure 11).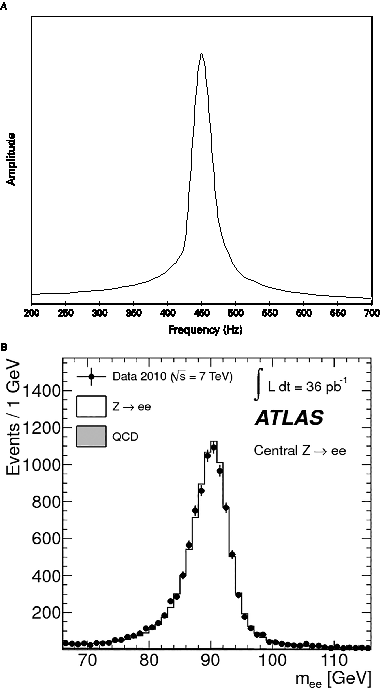
Figure 11. Two examples of resonance: (a) resonance of a wine glass at its natural frequency of 454.73 Hertz, plotting the amplitude of the glass’s motion versus the frequency of the sound exciting it; (b) resonance showing the detection by the ATLAS collaboration at CERN of Z neutral intermediate bosons (mass 90 GeV) by their decay into an electron-positron pair, plotting the number of detected events versus the invariant mass-energy of the observed electron-positron pair. (Courtesy ATLAS collaboration).
I will close with the recent discovery of gravitational waves by the twin detectors of LIGO in Washington and Louisiana, each composed of 4 km long L-shaped vacuum tubes capable of registering minute vibrations (figure 12). On September 14, 2015, both detectors simultaneously registered the passage of vibrations that strongly indicated as their source two merging black holes about 1.3 billion light years distant. The signal was recorded as a “chirp” played around the world, a swooping glissando that came up to about middle C on the piano. As the LIGO team emphasized in its public announcements, their instruments were “blind,” not registering any form of light or radiation but rather “feeling” the vibrations caused in the fabric of spacetime by gravitational waves emanating from a far-distant source. Thus, though no sound traveled directly, the gravitational waves were detected as vibrations and, in that metaphorical sense, were “heard” rather than “seen.” The constant description of these events as “chirps” was a powerful reminder of the connection between vibrating bodies and the confirmation of Albert Einstein’s gravitational waves a century after he first proposed them.
Figure 12. The two LIGO gravitational wave interferometers at Hanford, WA and Livingston, LA. (Courtesy LIGO)
Even beyond this spectacular result, the ancient project to mathematize nature through the intermediacy of music continues to thrive. Arguably, modern science is for our civilization what the Pyramids were for ancient Egypt or the cathedrals for medieval Europe: the great cultural project of the time. Compared to them, the “invisible pyramid” of modern science (as Loren Eiseley called it) is not a static artifact or construction but continues and develops with all the dynamism of music.
About the Author
Peter Pesic is director of the Science Institute and Musician-in-Residence at St. John’s College, Santa Fe. He is the author of Labyrinth: A Search for the Hidden Meaning of Science; Seeing Double: Shared Identities in Physics, Philosophy, and Literature; Abel’s Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability; Sky in a Bottle; Music and the Making of Modern Science; and Polyphonic Minds: Music, Science, and Expression (to appear fall 2017).


